前回の続きです。
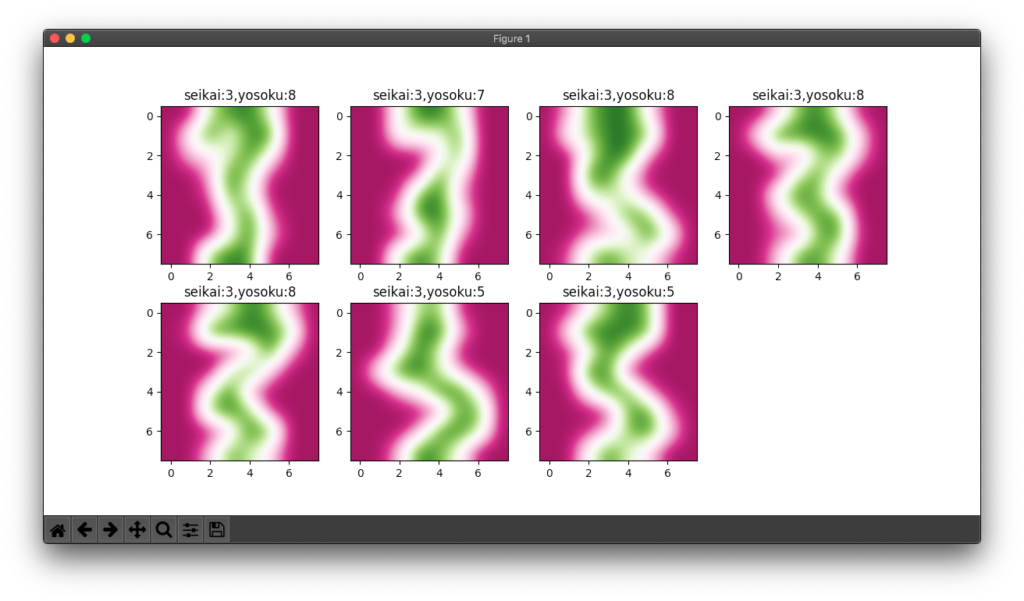
不正解が多かった3の該当画像を一括表示しました。確かに間違えやすい書き方だということが分かります。
from sklearn import datasets
import sklearn.svm as svm
import matplotlib.pyplot as plt
# 手書き数字のデータをロード
digits = datasets.load_digits()
# 画像データを変数all_featuresに、画像内容(数字)を変数teacher_labelsに格納
all_features = digits.data
teacher_labels = digits.target
num_samples = len(all_features)
model = svm.SVC(gamma = 0.001)
# 学習用の学習データと正解データ(1500個)
train_features=all_features[ : 1500 ]
train_teacher_labels=teacher_labels[ : 1500 ]
print(len(train_features))
# 検証用の学習データと正解データ(297個)
test_feature=all_features[1500 : ]
test_teacher_labels=digits.target[1500 : ]
print(len(test_feature))
# 学習実行
model.fit(train_features,train_teacher_labels)
# 数値予測データと検証用画像データ
predicted = model.predict(test_feature)
test_images = digits.images[1500 : ]
# 図のサイズ設定
fig = plt.figure(figsize=(12, 6))
# 前回記事で不正解が多かった3の画像で不正解のものを表示する
i = 1
for la,pre,img in zip(test_teacher_labels,predicted,test_images):
if la == 3 and la != pre:
plt.subplot(2, 4, i)
plt.imshow(img, cmap='PiYG', interpolation='bicubic')
plt.title(f'seikai:{la},yosoku:{pre}')
i = i + 1
plt.show()